-
1.
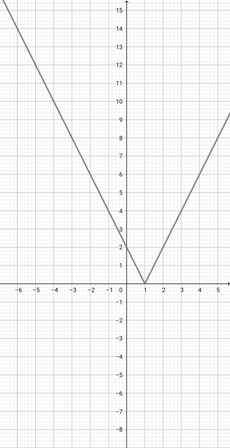
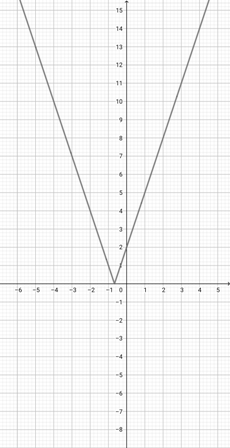
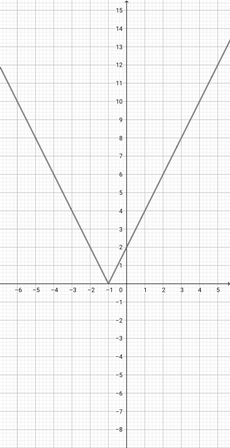
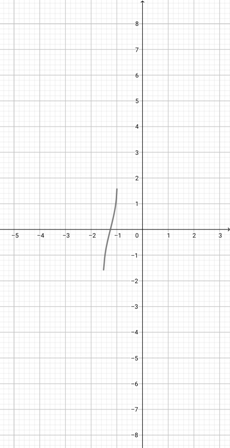
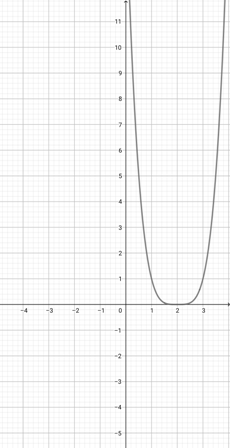
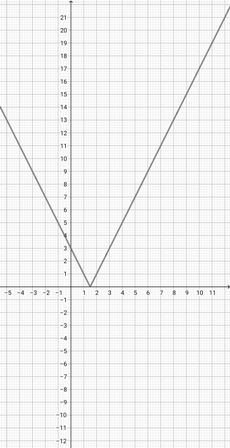
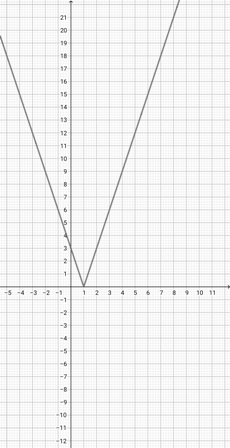
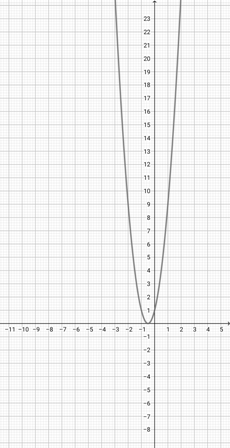
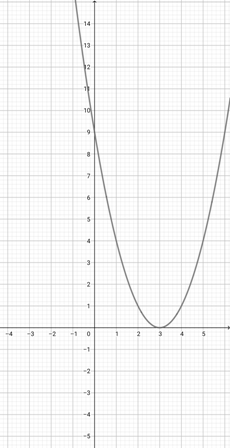
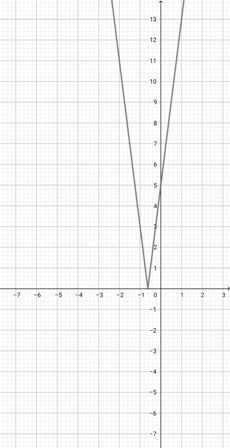
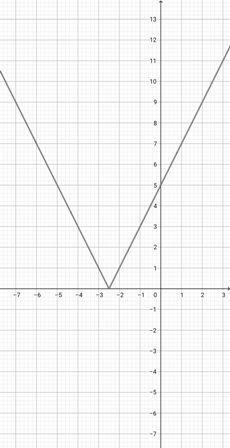
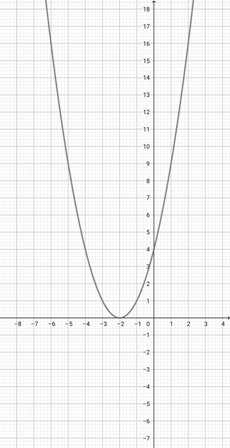
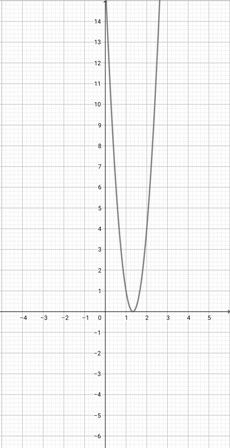
Use the graph of {eq}f(x)=\lvert x+2 \rvert {/eq} to select the graph of the function {eq}g(x)=\lvert 2x+2 \rvert {/eq}.
-
2.
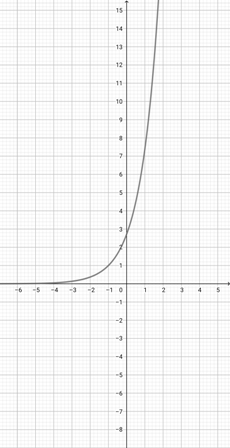
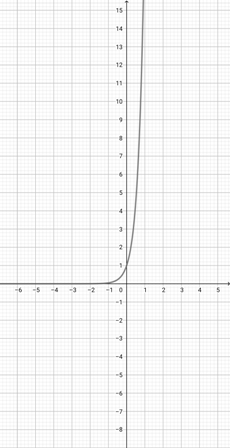
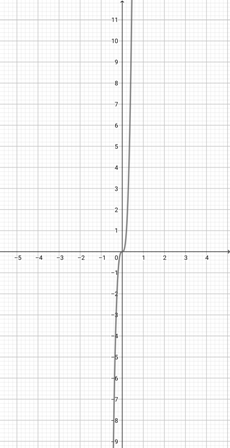
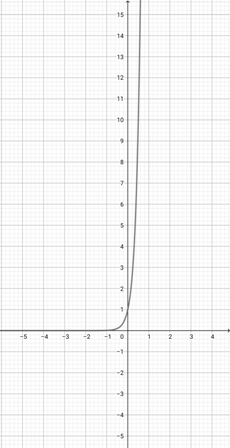
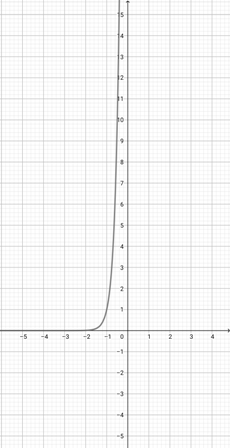
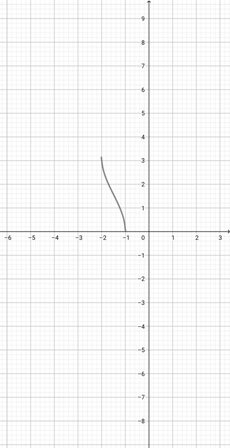
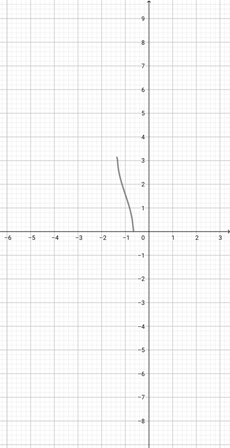
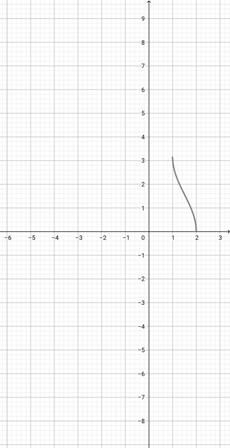
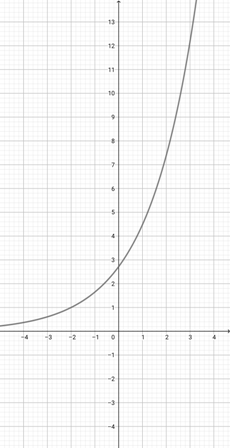
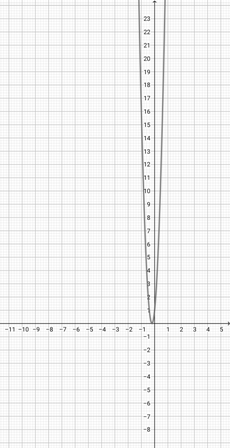
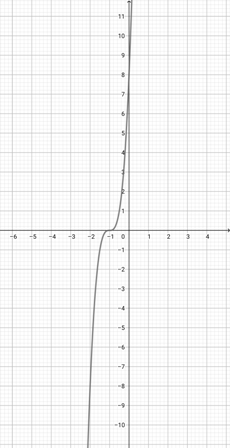
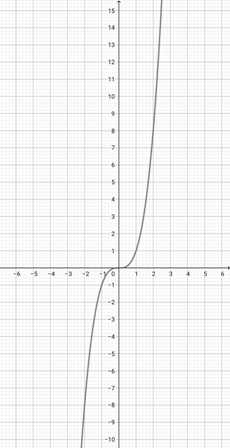
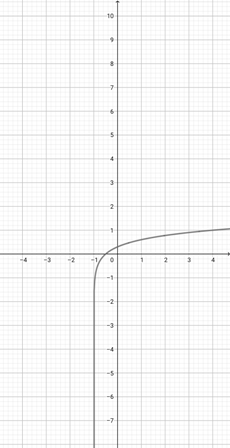
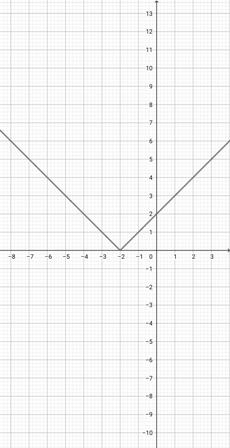
Given the graph of {eq}f(x)=e^{x} {/eq} below, graph the function {eq}h(x)=e^{3x} {/eq}.
-
3.
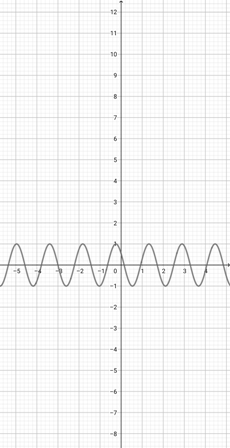
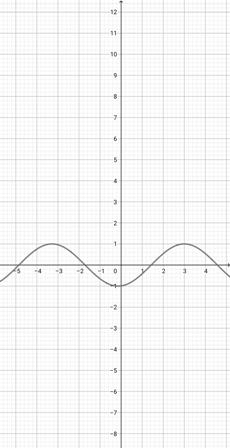
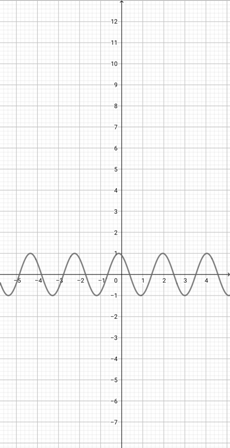
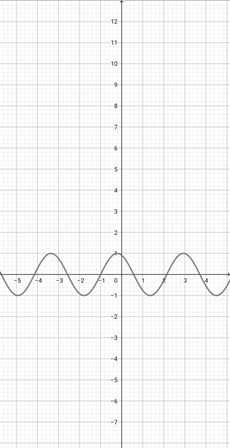
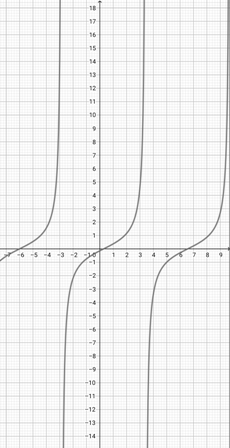
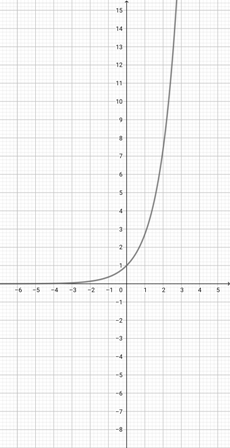
Using the graph of {eq}f(x)=\cos (x+1) {/eq} given below, determine the graph of the function {eq}z(x)=\cos (4x+1) {/eq}.
-
4.
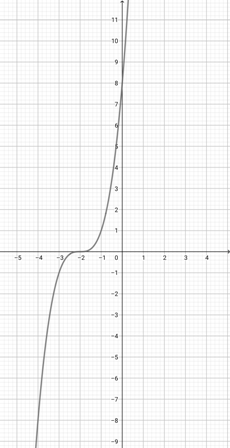
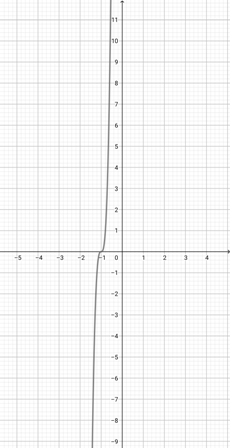
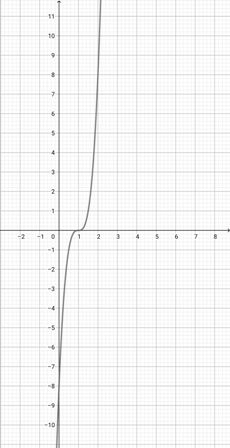
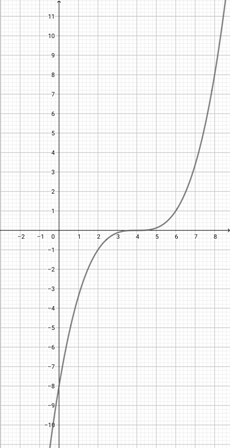
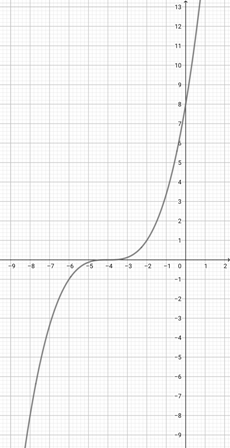
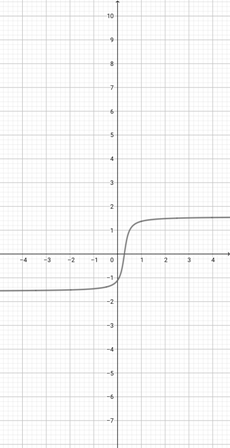
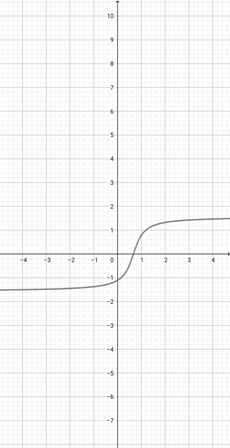
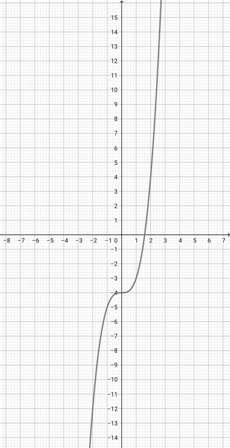
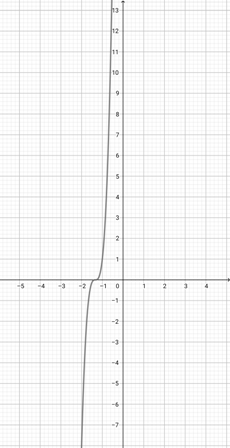
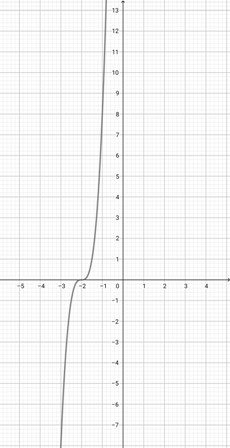
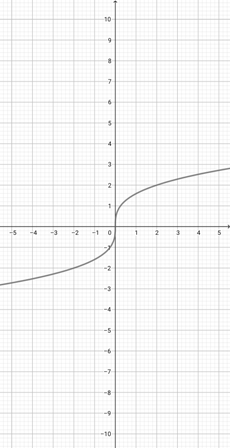
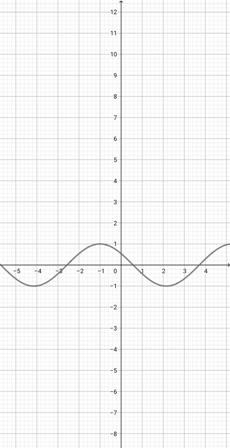
Given the graph of {eq}f(x)=x^{3} {/eq} below, plot the function {eq}a(x)=(5x)^{3} {/eq}.

-
5.
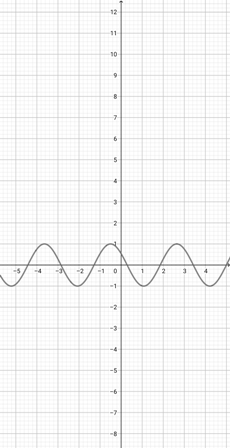
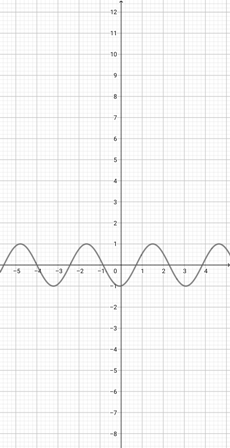
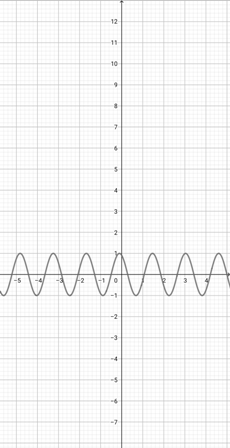
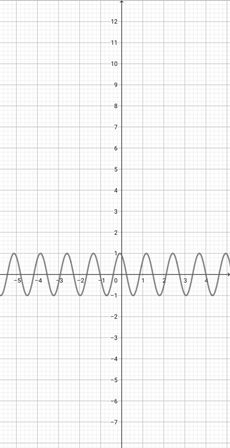
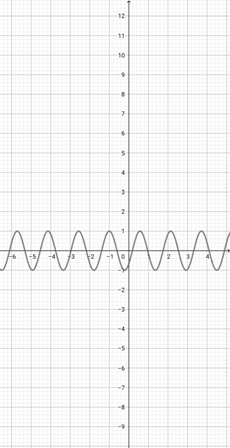
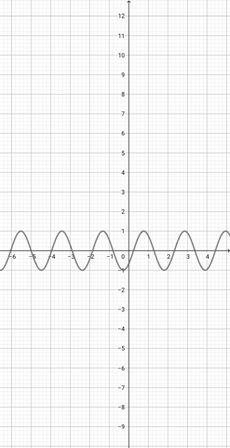
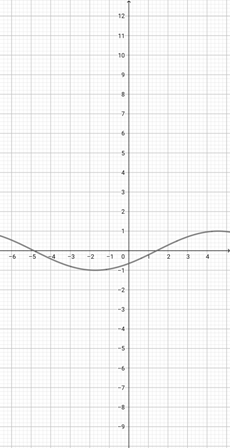
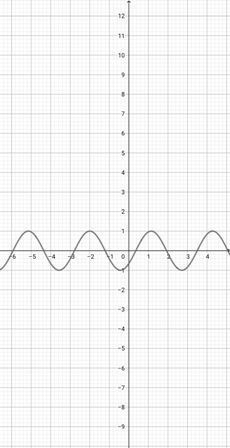
Using the graph of {eq}f(x)=\sin (x+2) {/eq} below, which of the following graphs is the correct graph of the function {eq}y(x)=\sin (2x+2) {/eq}?
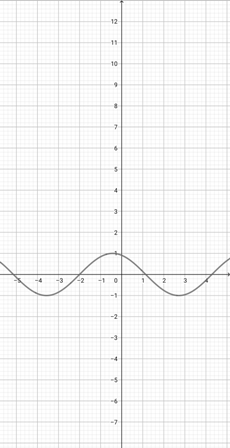
-
6.
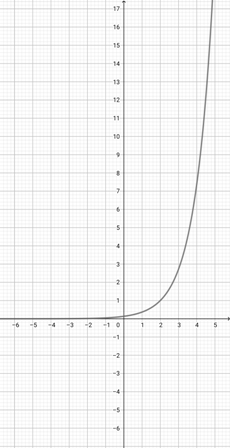
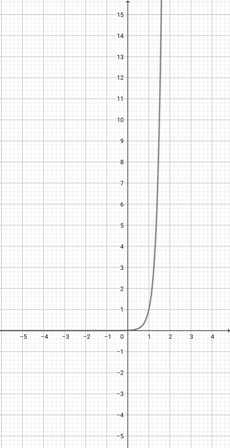
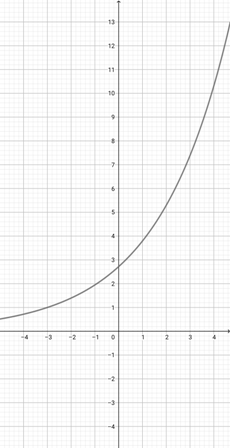
Use the graph of {eq}f(x)=10^{x} {/eq} to choose the graph of the function {eq}p(x)=10^{2x} {/eq}.
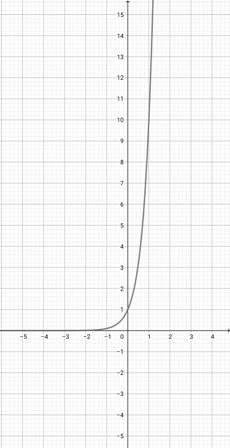
-
7.
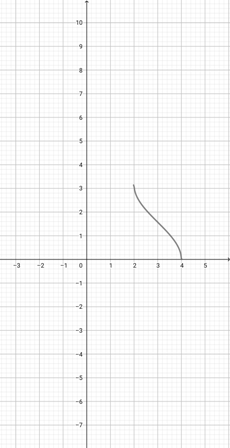
Given the graph of {eq}f(x)=\cos^{-1}(x+3) {/eq} below, graph the function that represents {eq}m(x)=\cos^{-1}(3x+3) {/eq}.
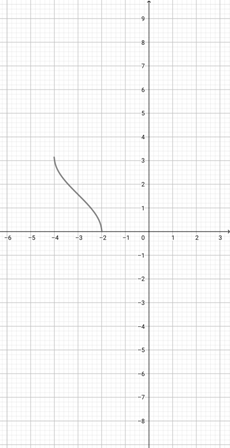
-
8.
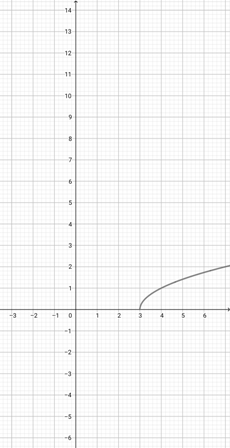
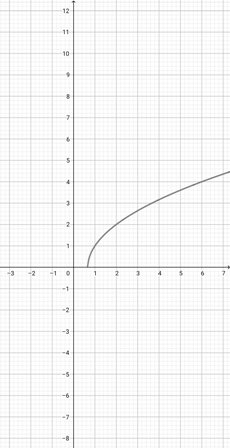
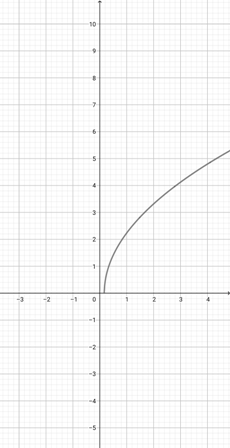
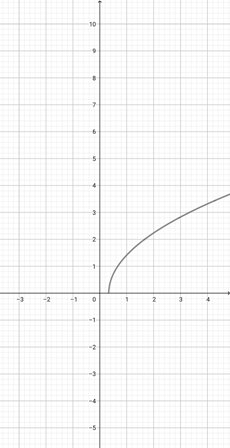
Using the graph of {eq}f(x)=\sqrt{x-2} {/eq} given below, identify the graph of the function {eq}k(x)=\sqrt{2x-2} {/eq}.
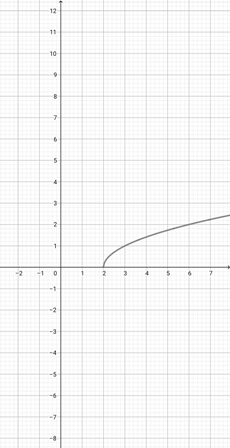
-
9.
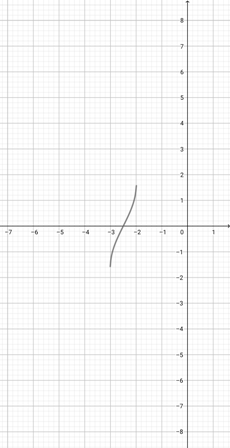
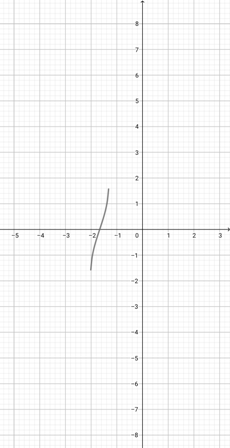
Given the graph of {eq}f(x)=\sin^{-1}(x+5) {/eq} below, represent the function {eq}r(x)=\sin^{-1}(2x+5) {/eq} graphically.
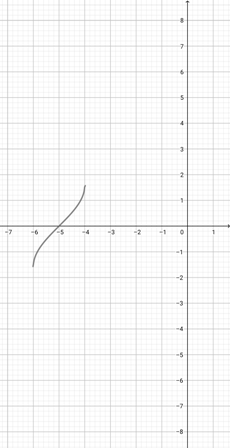
-
10.
Using the graph of {eq}f(x)=x^{4} {/eq} below, which of the following graphs is the correct graph of the function {eq}c(x)=(3x)^{4} {/eq}?
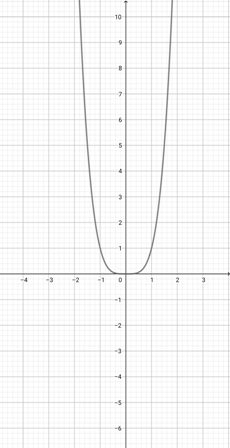
-
11.
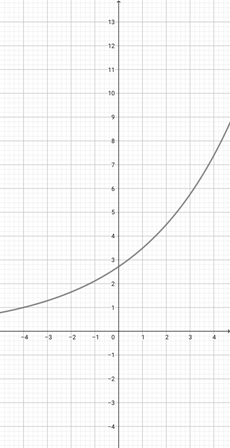
Use the graph of {eq}f(x)=e^{x+1} {/eq} to select the graph of the function {eq}g(x)=e^{\frac{x}{2}+1} {/eq}.
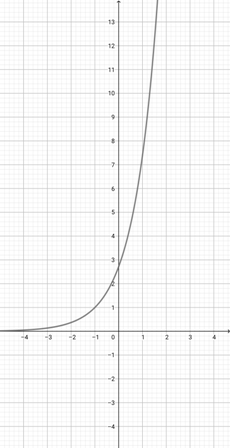
-
12.
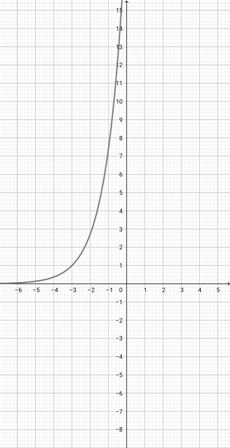
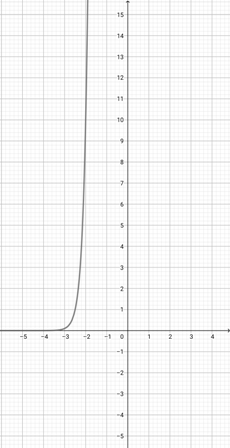
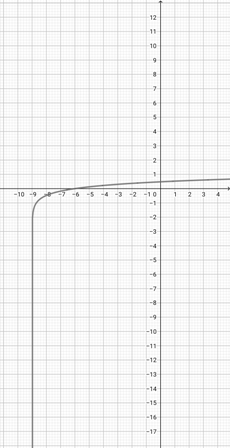
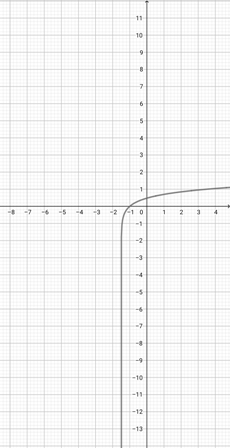
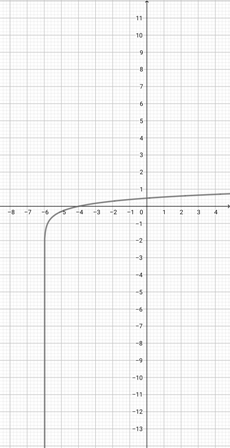
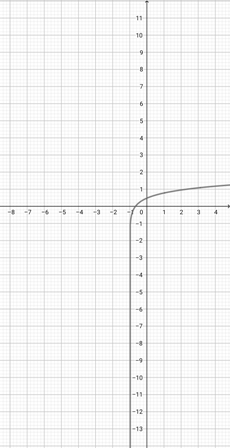
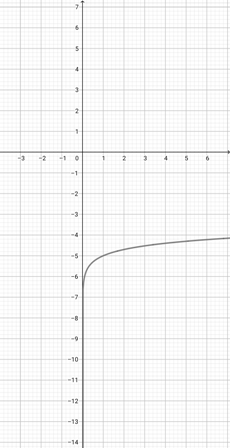
Given the graph of {eq}f(x)= \log (x+3) {/eq} below, graph the function {eq}h(x)=\log (\frac{x}{3}+3) {/eq}.
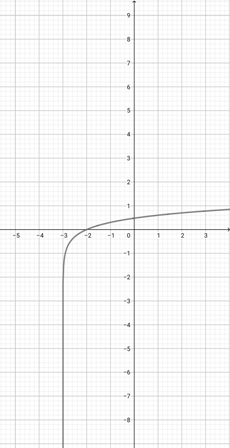
-
13.
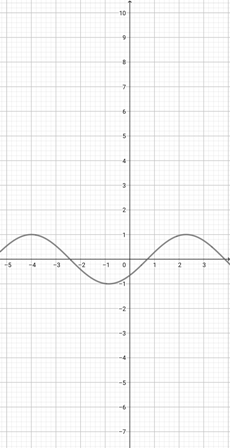
Using the graph of {eq}f(x)=\cos (x+4) {/eq} below, find which of the following four graphs is the correct representation of the function {eq}j(x)=\cos (\frac{x}{2}+4) {/eq}.
-
14.
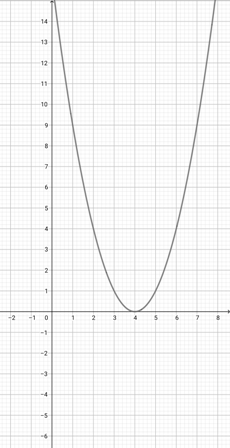
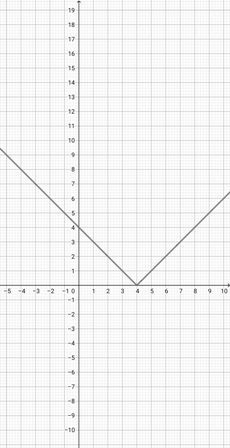
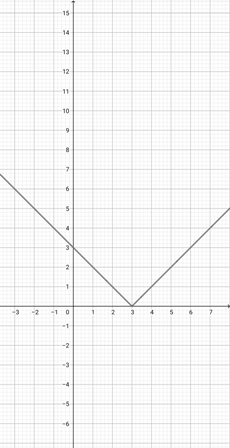
Given the graph of {eq}f(x)=\lvert x-3 \rvert {/eq} below, plot the function {eq}k(x)=\lvert \frac{x}{3}-3 \rvert {/eq} on the coordinate plane.
-
15.
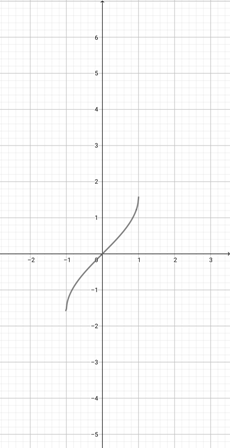
With the help of the graph of {eq}f(x)= \sin^{-1}x {/eq} given below, determine the graph of the function {eq}l(x)=\sin^{-1}(\frac{x}{2}) {/eq}.
-
16.
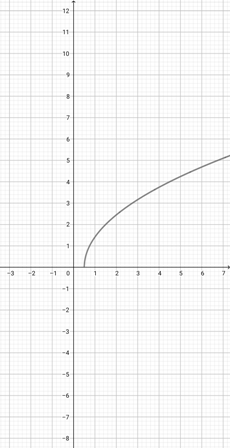
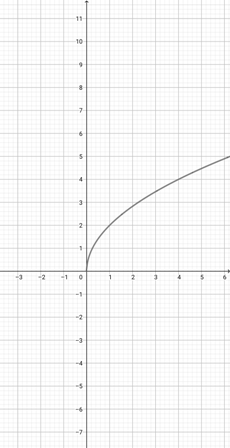
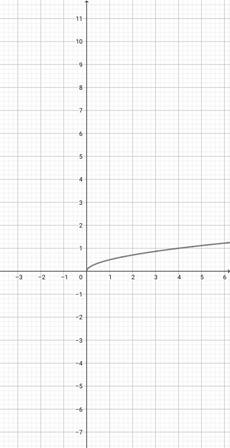
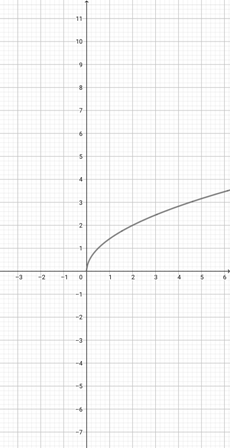
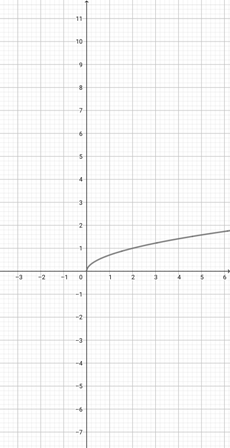
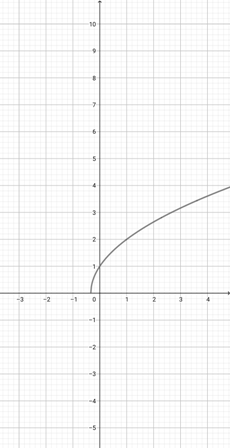
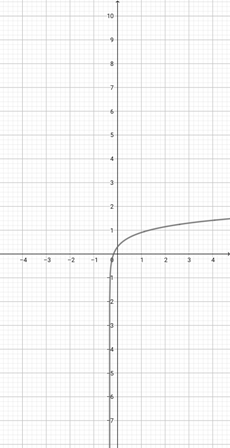
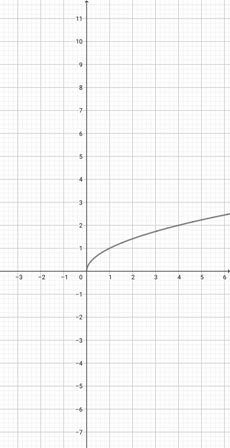
Use the graph of {eq}f(x)=\sqrt{x} {/eq} given below to choose the correct graphical representation of the function {eq}d(x)=\sqrt{\frac{x}{4}} {/eq}.
-
17.
Given the graph of {eq}f(x)=(x+4)^4 {/eq} below, represent the function {eq}s(x)=(\frac{x}{3} + 4)^4 {/eq} graphically.
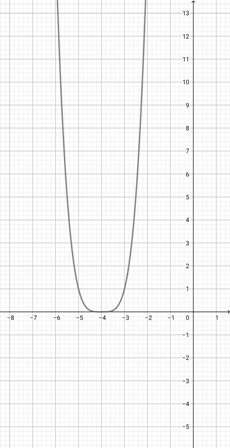
-
18.
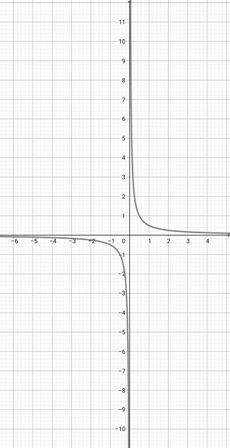
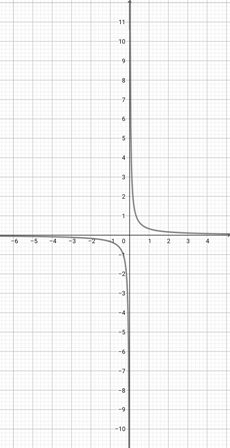
Using the graph of {eq}f(x)=\frac{1}{x} {/eq} below, find which of the following graphs is the correct graph of the function {eq}a(x)=\frac{1}{2x} {/eq}.

-
19.
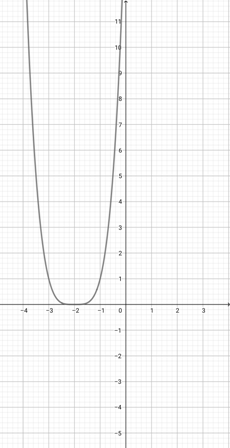
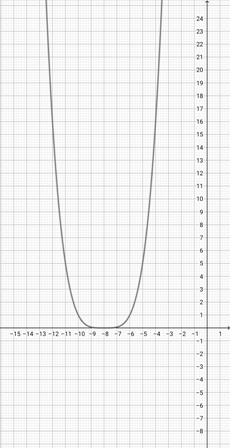
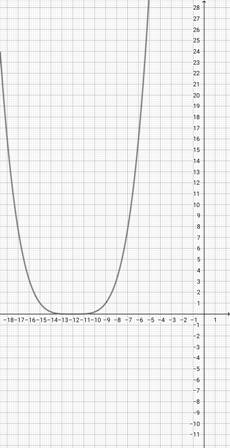
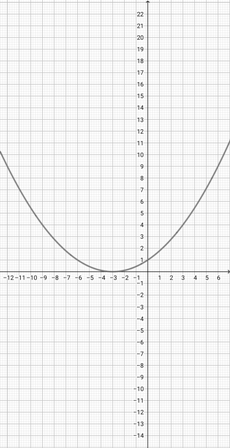
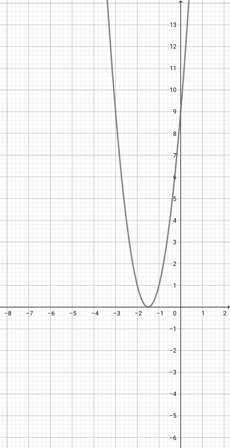
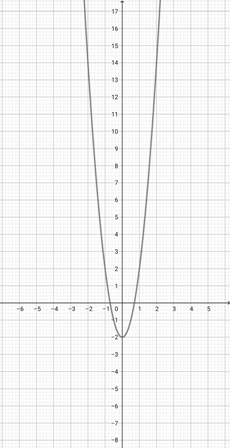
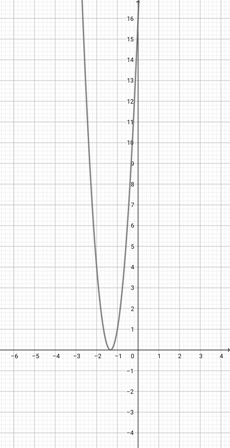
With the help of the graph of {eq}f(x)=(x+1)^{2} {/eq} given below, identify the graph of the function {eq}q(x)=(\frac{x}{3}+1)^{2} {/eq}.
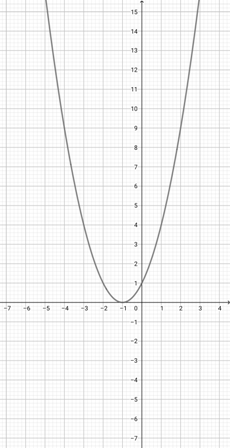
-
20.
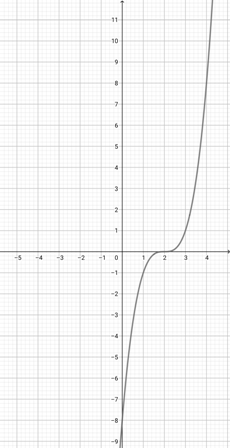
Use the graph of {eq}f(x)=(x-2)^{3} {/eq} below to graph the function {eq}w(x)=(\frac{x}{2}-2)^{3} {/eq}.
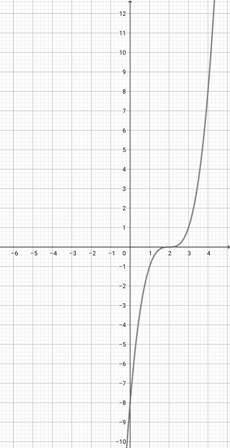
-
21.
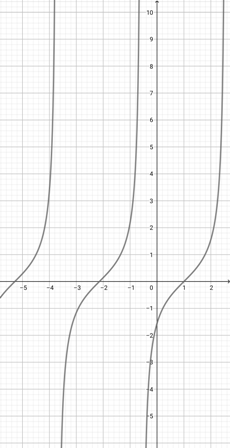
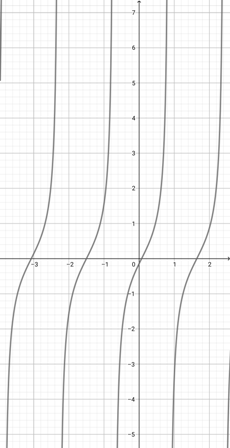
Use the graph of {eq}f(x)= \tan (x+3) {/eq} to select the graphical representation of the function {eq}a(x)=\tan (2x+3) {/eq}.
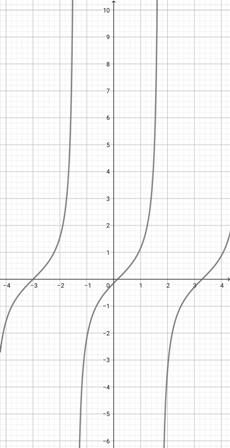
-
22.
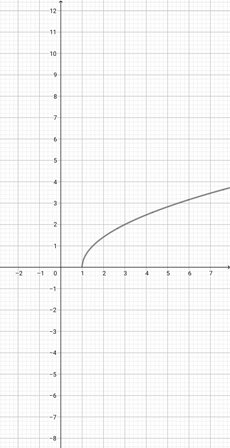
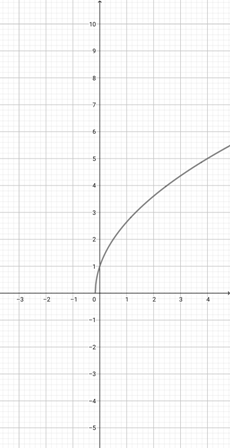
Given the graph of {eq}f(x)= \sqrt{x+1} {/eq} below, plot the function {eq}g(x)=\sqrt{3x+1} {/eq}.
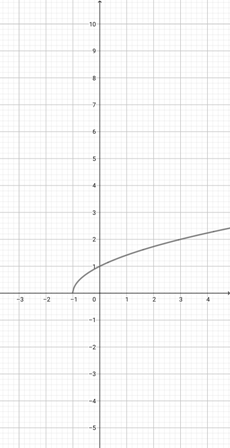
-
23.
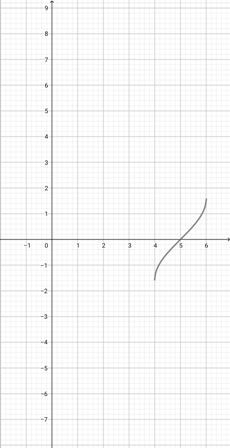
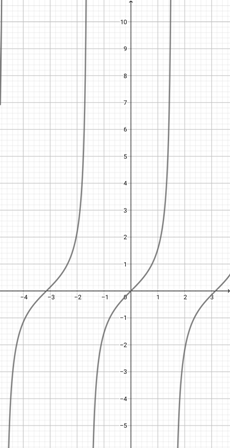
Using the graph of {eq}f(x)= \tan^{-1}(x-2) {/eq} shown below, find the correct representation of the function {eq}z(x)=\tan^{-1}(3x-2) {/eq}.
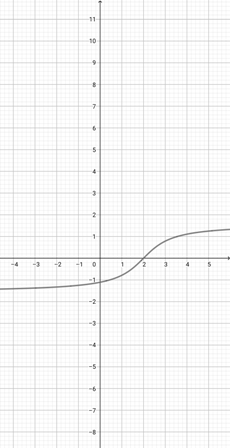
-
24.
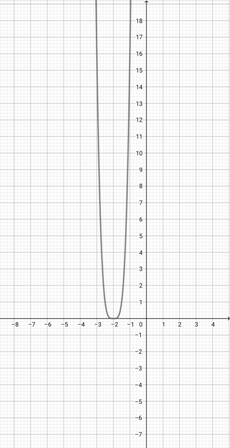
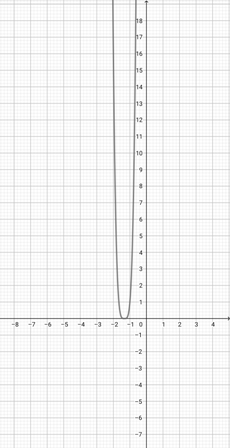
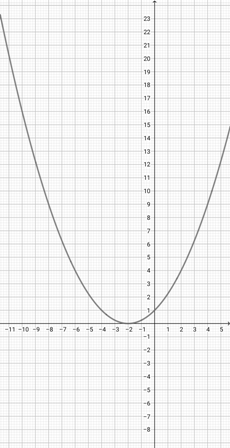
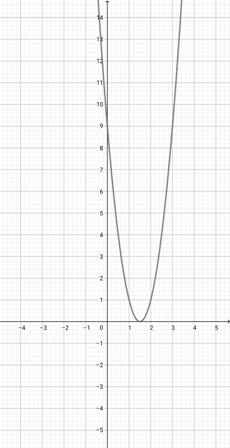
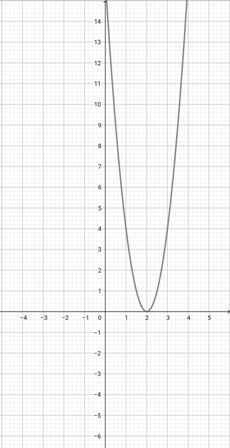
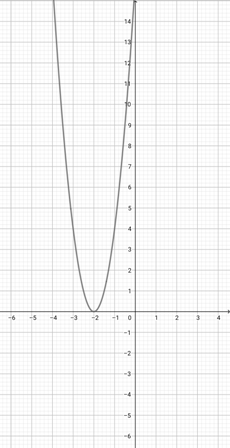
Given the graph of {eq}f(x)=(x+3)^{2} {/eq} below, plot the function {eq}y(x)=(2x+3)^{2} {/eq} on the coordinate axes.
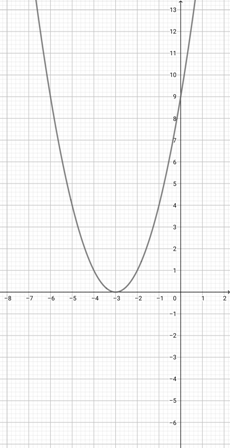
-
25.
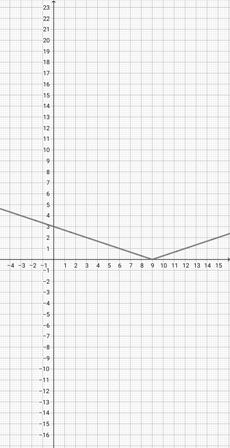
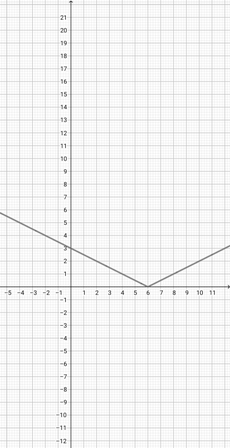
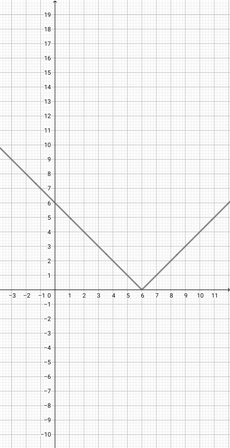
With the help of the graph of {eq}f(x)= \lvert x+5\rvert {/eq} given below, determine the scaled graph of the function {eq}k(x)= \lvert 2x+5\rvert {/eq} from it.
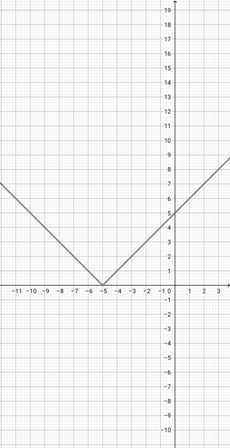
-
26.
Use the given graph of {eq}f(x)=(x+4)^{3} {/eq} and choose the graphical representation of the function {eq}p(x)=(3x+4)^{3} {/eq}.
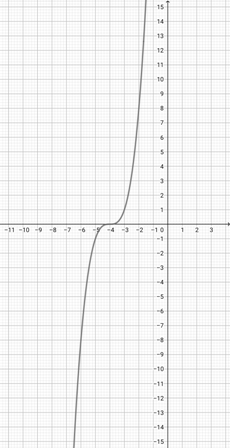
-
27.
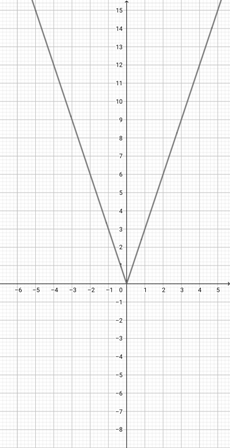
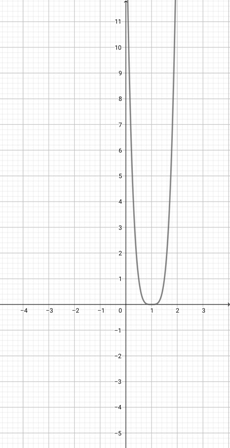
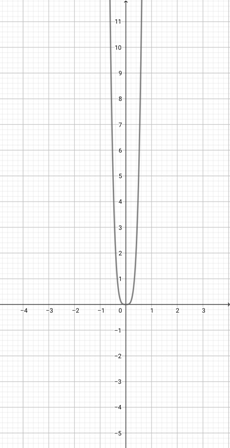
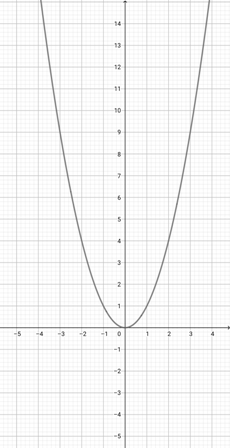
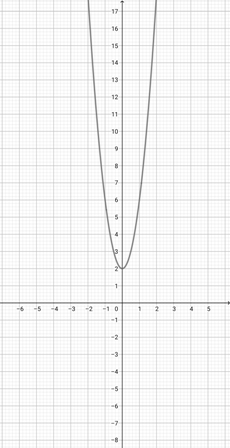
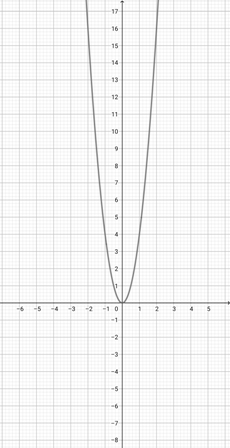
Given the graph of {eq}f(x)=x^{2} {/eq} below, represent the function {eq}o(x)=(2x)^{2} {/eq} graphically.
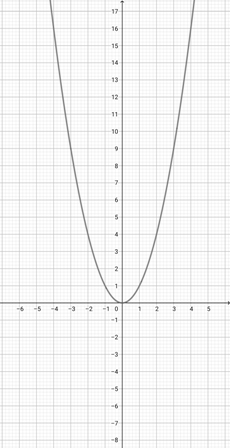
-
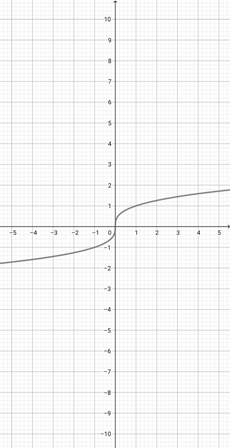
28.
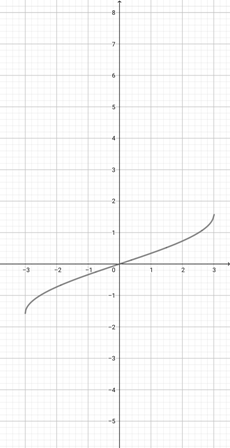
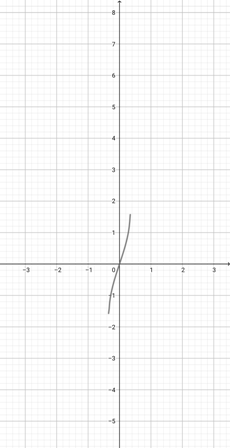
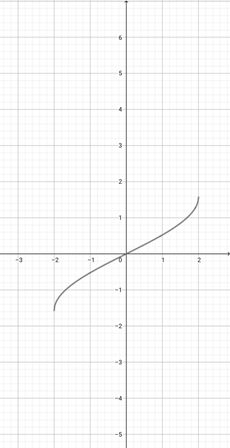
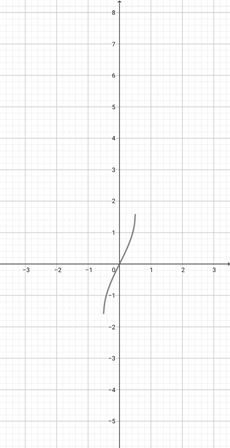
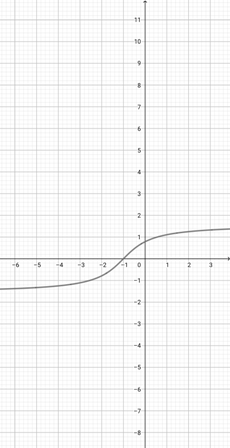
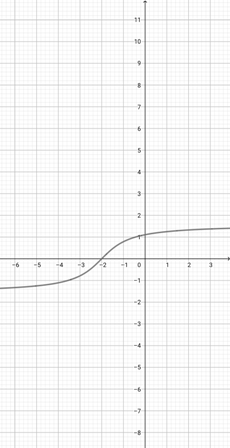
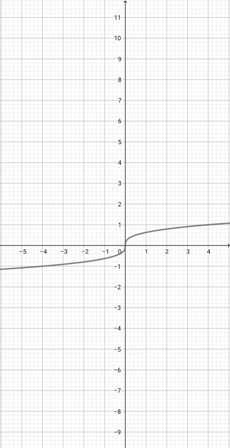
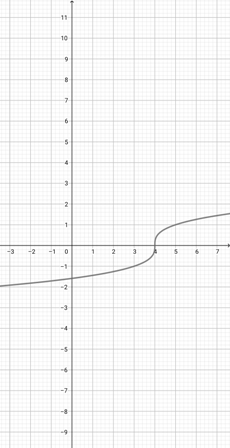
Using the following graph of {eq}f(x)=x^{\frac{1}{3}} {/eq}, find the equivalent graph of the function {eq}l(x)=(4x)^{\frac{1}{3}} {/eq}.
-
29.
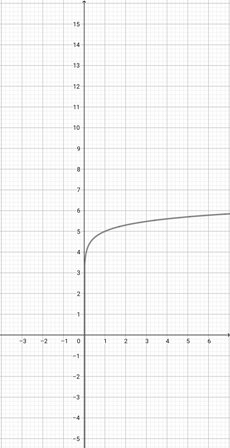
With the help of the given graph of {eq}f(x)= \log (x+2) {/eq}, identify the scaled graph of the function {eq}n(x)=\log (2x+2) {/eq} from it.
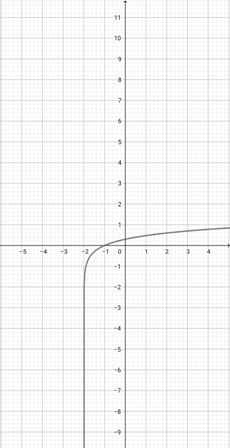
-
30.
Use the graph of {eq}f(x)=(x-4)^{2} {/eq} below to graph the function {eq}j(x)=(3x-4)^{2} {/eq}.