 |
The Platonic solids are a group of five polyhedra, each having identical faces that meet at identical angles. Some of the earliest records of these objects are referenced by Euclid around 300 BCE in Alexandria, Egypt, from his mention of the Athenian mathematician Theaetetus' work. Still older records exist from Pythagoras, another Greek mathematician who concerned himself with geometrical shapes.
The Platonic solids are named after Plato, however. In his work Timaeus, he associates five regular polyhedra to fire, earth, air, water, and heaven. He used these shapes and their assumed association with these elements to create a theory of the universe, and through this theory these polyhedra became associated with his name.
The Platonic solids are all regular polyhedra. This means that each Platonic solid is composed of identical faces and angles on each solid's surface. A polyhedron is a three-dimensional geometric object with flat faces on its surface that are polygons. Polygons are flat, two-dimensional shapes consisting of at least three straight edges that meet at points known as vertices.
According to Plato, each Platonic solid was associated with an element. The tetrahedron, with four triangular faces creating a pyramid, was related to fire due to its steep, pointy angles. The cube, with squares for faces, was associated with earth. The octahedron's eight triangular faces were associated with air. The icosahedron, with twenty triangular faces, became associated with water. Finally, the dodecahedron, with twelve pentagonal faces that Plato claimed were related to the twelve constellations, was assigned a relationship to the heavenly realms.
The five Platonic solids have been used and are in use all over the world due to their "perfect" nature. They hold an appeal in terms of mathematical precision as well as in their symmetrical nature that is often considered attractive for a variety of reasons.
One example is their use in dice. The most common dice are in the form of a cube, but tabletop games often use tetrahedral, octahedral, dodecahedral, and icosahedral dice as well.
Another example of Platonic solid use is in computer-assisted three-dimensional modeling. Due to the nature of graphics chipsets being optimized for triangular calculations, octahedra and icosahedra are common base shapes to create spheres from, and cubes (with square faces easily created from pairs of triangles) are famously used in the popular videogame Minecraft.
The Kaaba, the cuboid building at the center of the Great Mosque of Mecca and whose name translates literally to "The Cube", is the most sacred physical site to the Islamic religion. Renaissance artists thought the Platonic solids provided excellent demonstrations of symmetry and applied the solids' geometries to provide perspective in their art. The Pyramids of Giza are perfect halves of octahedra, or pyramids with square bases.
 |
A tetrahedron is described as a regular polyhedron whose vertices are created by three equilateral triangles meeting at their corners. The prefix tetra- means four, which stands for the four faces of the object.
 |
A cube, which is also called a hexahedron, is described as a regular polyhedron whose vertices are created by three squares meeting at their corners. The prefix hexa- means six, which stands for the six faces of a hexahedron. This is also the only Platonic solid that is created with square faces, due to squares having internal angles of 90 degrees. To construct a regular polyhedron from squares limits the number of faces meeting at vertices to three, as four meeting at a vertex would total their angles to 360 degrees and result in a flat object.
 |
An octahedron is an object whose vertices are the corners of four equilateral triangles. The prefix octa- stands for eight, which is the number of faces of this solid.
 |
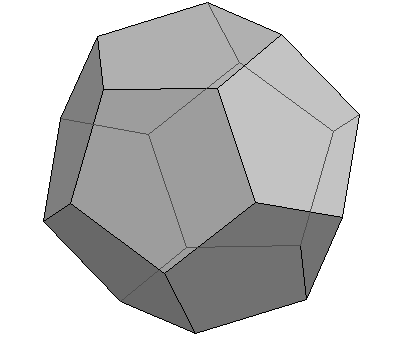A dodecahedron is the only Platonic solid whose faces are composed of pentagons, with vertices created by three pentagons meeting at their corners. The prefix dodeca- stands for twelve, which is the number of faces of the object. Like the cube with its square faces, no other regular polyhedron can be constructed with pentagon faces, as the internal angles of four or more meeting would be equal to or greater than 360 degrees.
 |
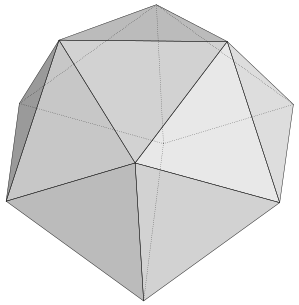An icosahedron is characterized by five equilateral triangles meeting at its vertices. The prefix icosa- stands for twenty, which is the number of faces of an icosahedron.
A regular polyhedra must have interior angles of polygon faces meeting at vertices that total less than 360 degrees. If interior angles added up to exactly 360 degrees, the object would no longer be a polyhedron, as it would be a flat object and no longer three-dimensional. If the interior angles added to greater than 360 degrees, the shape would no longer be convex. Its surface would be curved in the wrong direction and the surface would not be on the polyhedron's "outside". This limits the potential number of regular polydehra to the five Platonic solids due to the math surrounding their interior polygonal angles.
This table describes the total vertices, edges, and faces of each Platonic solid.
| Platonic solid | Faces | Vertices | Edges |
|---|---|---|---|
| Tetrahedron | 4 | 4 | 6 |
| Cube | 6 | 8 | 12 |
| Octahedron | 8 | 6 | 12 |
| Dodecahedron | 12 | 20 | 30 |
| Icosahedron | 20 | 12 | 30 |
Euler's formula describes a property of all polyhedra, which can also be applied to regular polyhedra, or Platonic solids.
{eq}F + V - E = 2 {/eq}
This formula states that the total number of faces of a polyhedron plus its total vertices, minus its total edges, will always equal two.
As an example, a tetrahedron has four faces plus four vertices, minus six edges, which equals two.
A dodecahedron has twelve faces plus twenty vertices, minus thirty edges, which likewise equals two.
Repeating this process with the properties of each Platonic solid will always produce a result of two.
The Platonic solids are a group of five polyhedra, each having identical faces that meet at identical angles. The Platonic solids are named after Plato, who associated them with elements in his theory of the universe. A polyhedron is a three-dimensional geometric object with flat faces on its surface that are polygons. Polygons are flat, two-dimensional shapes consisting of at least three straight edges that meet at points known as vertices. Tetrahedra have four faces, cubes or hexahedra have six faces, octahedra have eight faces, dodecahedra have twelve faces, and icosahedra have twenty faces. Regular polyhedra (the Platonic solids) must have interior angles of polygon faces meeting at vertices that total to less than 360 degrees, which limits the total number of them to five. Euler's formula can be used to verify that a combination of faces, vertices, and edges results in a valid polyhedron.
What defines a platonic solid? A platonic solid is a three-dimensional shape whose faces are all the same shape and whose corners are the meeting place of the same number of polygons. Okay, so this sounds like a complicated definition, but it really isn't. Once you see the shapes, you will easily understand. There are only five platonic solids in the whole world. Let's see what they look like and a real-world example of each.
A tetrahedron is a platonic solid made from triangles and has three sides meeting at every corner. You can see below that this shape is made from a total of four triangles all connected to each other. There are four corners, and you can count three triangle sides coming together at every corner. This is what being a platonic solid is all about, and you will see that all the other shapes are similar, just with different shapes and different numbers of sides meeting at each corner.
 |
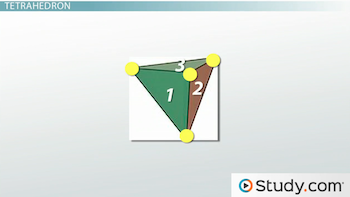Where can you expect to see a tetrahedron in the real world? You can see one in some games that use a four-sided die.
Next one up is the hexahedron, otherwise called a cube. It is a platonic solid made from squares and has three sides meeting at each corner. This particular solid is made from a total of six squares, and you can see below that at each of the eight corners there are three square sides coming together.
 |
The cube, or hexahedron, is a popular solid in the world. You see it in ice cubes and also in the traditional six-sided playing dice.
An octahedron is a platonic solid whose sides consist of triangles and that has four triangle sides meeting at every corner. It has a total of eight triangle sides and six corners where four triangles meet.
 |
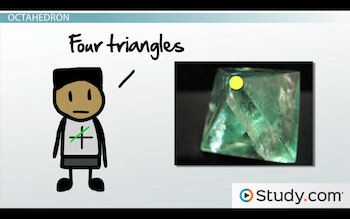You can find an octahedron in minerals such as fluorite. Looking at this fluorite above, at the top corner, do you see how many triangles are meeting together? That's right; there are four triangles, and we are consistent with the definition of this shape.
Another platonic solid is the dodecahedron, which is a platonic solid that has pentagons for its sides and that has three pentagon sides meeting at every corner. This solid has a total of twelve pentagons and twenty corners.
 |
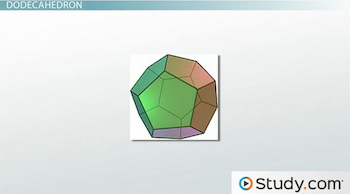In the real world, you will see dodecahedrons as fancy playing dice in some games. Usually, these are role-playing games that require a twelve-sided die.
The last of the platonic solids is the icosahedron, a platonic solid with triangles for sides and that has five triangle sides meeting at every corner. This particular solid has a total of twenty triangles and twelve corners. This platonic solid has the largest number of sides out of all the others.
 |
Here again, you can find icosahedrons at work in the game world. In a fairly popular word board game, you will find the icosahedrons used as playing dice in choosing a random letter to work with. In the microscopic world, you can find icosahedrons under the microscope when you look at some viruses, such as the herpes virus.
In this video lesson, we have seen all the platonic solids that exist in the world. We learned that platonic solids are three-dimensional solids that have the same polygon for all its sides and that have the same number of sides coming together at each corner. We learned there are only five platonic solids in the whole world.
The first is the tetrahedron, which is made of triangle faces and that has three triangle sides coming together at each corner. The hexahedron, or cube, has squares for its sides and has three square sides coming together at each corner. The octahedron has triangle sides and has four triangle sides coming together at each corner. The dodecahedron is made of pentagon sides and has three pentagons meeting at every corner. The icosahedron has triangles for its sides and has five triangle sides at every corner. Most of these occur in the real world as playing dice, but some you can find under the microscopic world as well.
When you finish watching this video lesson, you could be ready to:
Become a Study.com member and start learning now.
Become a MemberAlready a member? Log In
Back
I would definitely recommend Study.com to my colleagues. It’s like a teacher waved a magic wand and did the work for me. I feel like it’s a lifeline.
There are only five Platonic solids due to their requirement of having equal polygonal faces whose internal angles total less than 360 degrees when the angle is multiplied by the number of polygons that meet at the solid's vertices.
A tetrahedron has four faces made of equilateral triangles. A cube has six faces made of squares. An octahedron has eight faces made of equilateral triangles. A dodecahedron has twelve faces made of pentagons. An icosahedron has twenty faces made of equilateral triangles.
Platonic solids are a special set of polyhedra that have faces made of identical polygons, which are either equilateral triangles, squares, or pentagons.
A Platonic solid is one of five regular polyhedra that consist of identical polygonal faces whose corners meet at vertices made of equal angles.
Platonic solids have equal polygonal faces that meet at equal angles at their vertices and which create a convex polyhedron.
