Using Similarity Transformations with Similar Triangles

Using Similarity Transformations with Similar Triangles - Dilation

Step 1: Determine the center of dilation by finding which vertex does not move under the transformation.

Step 2: Find the scale factor that will transform one triangle into the other by finding what constant multiplied onto the side lengths of the original triangle results in the side lengths of the transformed triangle.

Using Similarity Transformations with Similar Triangles - Dilation: Vocabulary

Similarity Transformation: A similarity transformation takes one triangle and creates a similar triangle. Similar triangles have congruent angles, and the ratios of corresponding sides are constant.

Dilation: A dilation is a similarity transformation in which a triangle is expanded or contracted by a scale factor. All angles are kept the same, but side lengths are multiplied by a constant.

Center of Dilation: The center of dilation is a point that stays stationary under the dilation - all other points are moved farther away or closer to the center of dilation.

We will use these steps and definitions to use similarity transformations with similar triangles in the following two examples.

Using Similarity Transformations with Similar Triangles - Dilation: Example Problem 1

In the figure below,

• {eq}|AB| = 16 {/eq}, {eq}|BC| = 20 {/eq}, and {eq}|AC| = 12 {/eq}

• {eq}|A'B'| = 12 {/eq}, {eq}|B'C'| = 15 {/eq}, and {eq}|A'C'| = 9 {/eq}.

Find the dilation that transforms {eq}\Delta ABC {/eq} into {eq}\Delta A'B'C' {/eq} by identifying the center and the scale factor.

Image for Example 1

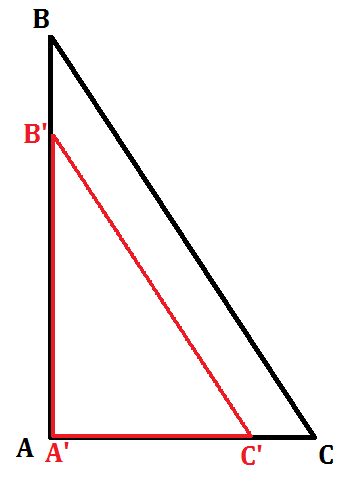Step 1: Determine the center of dilation by finding which vertex does not move under the transformation.

Since vertex {eq}A {/eq} and vertex {eq}A' {/eq} are in the same location, the center of dilation is vertex {eq}A {/eq}.

Step 2: Find the scale factor that will transform one triangle into the other by finding what constant multiplied onto the side lengths of the original triangle results in the side lengths of the transformed triangle.

We need to know what constant multiplied onto each side length of {eq}\Delta ABC {/eq} results in the corresponding side length of {eq}\Delta A'B'C' {/eq}. We will call the constant {eq}k {/eq}.

Using {eq}|AB| = 16 {/eq} and {eq}|A'B'| = 12 {/eq}, we have:

{eq}\begin{align} k\cdot 16 {}&= 12\\ k & = \dfrac{12}{16}\\ k & = \dfrac{3}{4} \end{align} {/eq}

To verify this is the scale factor, we will multiply the remaining side lengths of {eq}\Delta ABC {/eq} by {eq}k = \dfrac{3}{4} {/eq} to see if the results are the corresponding side lengths of {eq}\Delta A'B'C' {/eq}.

{eq}\begin{align} \dfrac{3}{4} |BC| {}& = \dfrac{3}{4}(20)\\ & = \dfrac{60}{4}\\ & = 15\\ & = |B'C'| \end{align} {/eq}

and

{eq}\begin{align} \dfrac{3}{4} |AC| {}& = \dfrac{3}{4}(12)\\ & = \dfrac{36}{4}\\ & = 9\\ & = |A'C'| \end{align} {/eq}

Therefore, a dilation with center {eq}A {/eq} and scale factor {eq}\dfrac{3}{4} {/eq} will transform {eq}\Delta ABC {/eq} into {eq}\Delta A'B'C' {/eq}.

Using Similarity Transformations with Similar Triangles - Dilation: Example Problem 2

In the figure below,

• {eq}|AB| = 5 {/eq}, {eq}|BC| = 5 {/eq}, and {eq}|AC| = 4 {/eq}

• {eq}|A'B'| = 10 {/eq}, {eq}|B'C'| = 10 {/eq}, and {eq}|A'C'| = 8 {/eq}.

Find the dilation that transforms {eq}\Delta ABC {/eq} into {eq}\Delta A'B'C' {/eq} by identifying the center and the scale factor.

Image for Example 2

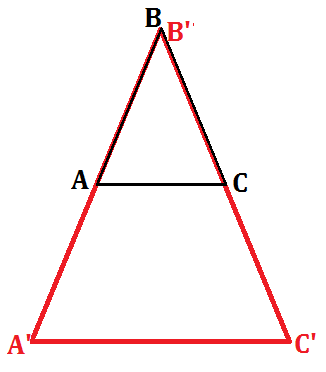Step 1: Determine the center of dilation by finding which vertex does not move under the transformation.

The center of dilation is vertex {eq}B {/eq}.

Step 2: Find the scale factor that will transform one triangle into the other by finding what constant multiplied onto the side lengths of the original triangle results in the side lengths of the transformed triangle.

Using {eq}|AB| = 5 {/eq} and {eq}|A'B'| = 10 {/eq}, we have:

{eq}\begin{align} k\cdot 5 {}&= 10\\ k & =2 \end{align} {/eq}

Checking the other sides:

• {eq}2\cdot|BC| = 2\cdot 5 = 10 = |B'C'| {/eq}

• {eq}2\cdot|AC| = 2\cdot 4 = 8 = |A'C'| {/eq}

Therefore, a dilation with center {eq}B {/eq} and scale factor {eq}2 {/eq} will transform {eq}\Delta ABC {/eq} into {eq}\Delta A'B'C' {/eq}.