For this physics lab, you will need:
- A flywheel
- An axle for the flywheel
- A mount for the axle that will allow it to rotate
- A weight hanger
- Slotted weights
- A stop watch
- A meter ruler
- String
- Duct tape
- A protractor
Step 1: Assemble the equipment. The flywheel should be on the axle and the axle attached to its mount, allowing it to freely rotate. Put a piece of duct tape on the side of the flywheel so that you can more accurately see how it is spinning.
Step 2: Tie one end of a long piece of string to a stationary support near the axle, then wind the string around the axle until there is little free string remaining.
Step 3: Attach some weights to the weight hanger, and tie the other end of the string to the top of the hanger. The weight should be hanging not far below the axle.
Step 4: Measure the height of the hanging mass above the ground.
Step 5: Release the mass and let it fall under gravity. Start the stopwatch at the same time, and measure how long it takes to reach the ground. Repeat five times and note down your numbers.
Step 6: Calculate the average of your trials by adding up the numbers and dividing by five.
Step 7: Do another five trials, but this time focus on the flywheel. Use the piece of tape to measure how many times the wheel rotates during the motion. To make your number as accurate as possible, use the protractor to measure the starting and finishing positions. For example, perhaps your wheel rotated 6.25 times, because it rotated 6 full circles, and then finished 90 degrees beyond its starting position.
Step 8: Calculate the average of your trials by adding up the numbers and dividing by five.
Step 9: Use the ruler to measure the radius of the flywheel.
You can record your data in a table that looks something like this:
Example data table
 |
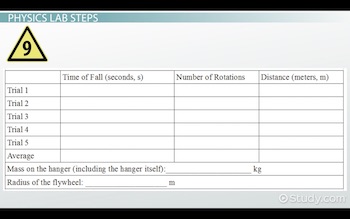If you haven't already, now it's time to pause the video and get started. Good luck!
